[10000ダウンロード済み√] ƒXƒpƒCƒ‰ƒ‹ƒp[ƒ} ‚­‚¹–Ñ ƒp[ƒ} ƒƒ“ƒY 133364

O n e c o p y o f a g f i r i P B o f e m a i l s (3 p a g e s ) f g i n c l u d e an e m a il fro m FBIHQ , C T D , d allefl L W /2 1 /2 0 0 5 to A SC , e t a l, b l b 6 b 7 C b 2 b 7 E D e ta ils (R' sclL aiL x i C fc S > b 6 b 7 C A L L I N F O R M A T I O N C O N T A I N E D± ¹ ¤ Ñ ² y ó S ý D P Ó ² ï S > ± ¹ ¤ Ñ ² y ó S ý P 8 & X Þ Ó î ± ¹ ¤ Ñ ² y ó S × ø À f O 7 ¹ ² S D ³ w 8 $ à j 5 ý w × Y º , D Ñ D D Ñ 3 ¯ ² d ± b ® Â S a ± ¹ D î ¨ à ² û À = á û S ( þ ² Ô É D ç $ 3 Þ¸ q y W , C N U ë b q O y r z u O } à { h P y W , ð ¬ < v o O q z F Ö ó z h P J Ã ¸ \ ¹ ñ ½ 3&5 ¹ ñ ½ ¤ ® T W , ¹ ñ ½ ¥ « = r y / g ( = W , ð y v \ b q U F Ö F Ö z W e y F Ö

Pdf A New Criterion For The First Case Of Fermat S Last Theorem

ƒXƒpƒCƒ‰ƒ‹ƒp[ƒ} ‚­‚¹–Ñ ƒp[ƒ} ƒƒ"ƒY

ƒXƒpƒCƒ‰ƒ‹ƒp[ƒ} ‚­‚¹–Ñ ƒp[ƒ} ƒƒ"ƒY-ç F ê = y p Z ¹ ñ ½ y ã è 0 O W # d 6,7 ñ û \ v Æ Á à \ , ê Ë ê = y p Z ¹ ñ ½ ã è v _ i t s _ ¢  Z ô O j b d } F ¹ ñ ½ Ü y6,7 ñ \ Ü ¯ ½ Ì W ¥ Ü b ã è 0 O W I X Z # d }Click here👆to get an answer to your question ️ If p(x) = x 3 , then p(x) p( x) is equal to

Altgr Key Wikipedia

P ∧ q ∴p, q p, q ∴p ∧ q p ∴p ∨q, q p p ∨ q , ¬p ∴q p, p → q ∴q p ⇒q ∴p → q Direct Proof Rule Not like other rules important application of inference rules • You can use equivalences to make substitutions of any subformula • Inference rules only can be applied to whole formulas (not correct otherwise) eg 1The result P ( Y ≤ 075 X = 05 ) = 5/6, mentioned above, is geometrically evident in the following sense The points (x,y,z) of the sphere x 2 y 2 z 2 = 1, satisfying the condition x = 05, are a circle y 2 z 2 = 075 of radius on the plane x = 05 The inequality y ≤ 075 holds on an arc The length of the arc is 5/6 of the lengthó ³ ¹ ñ ½ ³ Ö ¤ h Á c ¤ d Ü Ì V l ¥ r ð ¬ à s z ~ J Æ J Â ½ y J ~ À u r \ Ø d u t ¨ b d } à ¸ ¬ v U \ G S y Ê Y W 6 b j Î < r ~ _ Ù Þ Ø ¶ v ~ ° Õ F Õ Ö W , þ y G S y Ê Y z 6 b j } h y y

æ ä ù è P { ´ ä t ¢  ¯ · ' ® ¢ » t s ¹ Ñ ¼ y £ ´ c ¯ ü ù ó æ ä ù è P ´ Ô ® r % Û e · ³ Õ Ó â ° t ü ¨ ³ L Ë ' ­ 0 ® Ñ Ó ¨ Õ Ç ¨ u ° ¸ ~ ü ù ó æ ä ù è P ¢%18&Û « ³ £ ® r · Ö } Û Ë ´ Ì f · è ø % cIf X ~ B(n, p) and Y X ~ B(X, q) (the conditional distribution of Y, given X), then Y is a simple binomial random variable with distribution Y ~ B(n, pq) For example, imagine throwing n balls to a basket U X and taking the balls that hit and throwing them to another basket U Y If p is the probability to hit U X then X ~ B(n, p) is theTitle ã æ °ã è ªå® ã §ã ®å ¥åº·ã ã §ã 㠯表 æ§ å¼ 31()_xlsx Author i Created Date

Ê ª y % p ¹ Ñ Ä ¢ £ g Ö Ç Õ y &/% < v y Ñ ¹ » A ° ° A Ý Q ¤ ° å ó ¢ § Ì ;N p & U !ñ Á O Â y C n v " S J µ ¥ ­ b q O d } Ù þ Ù y T × s ¿ á ê ñ ¶ ` ê c q s v ë d ) Â i è y s v ,R7 y Õ v v Í u } q O d } ¸ 0 { Ì ¥ P Ð Ë Ñ ¤ c Ì I ² y W ' ñ û î P Æ Á ' ñ û î P ¤ ¼ è Â z P l ¥

Calameo ١٤ مختصر التحفة الاثنى عشرية

Formule Trigonometriche 047 Studocu

Page 5 Example HMM Rt1 P(Rt) T 07 F 03 Rt P(Ut) T 09 F 02 The Forward Algorithm Time/dynamics update and observation update in one recursive update Normalization Can be helpful for numerical reasonsAlternative form for quadratic equations We can also write the quadratic equation in the form y = a(x– p) 2 q The effect of p is still a horizontal shift, however notice that For p > 0, the graph is shifted to the right by p units For p < 0, the graph is shifted to the left by p units$4 !ý i ¹ } · Z Õ' Y Õ = E % E I 1 % (M)É ·Ñ ù & Y a(½ ñ *í æ ¹ ·} Ù ¹ a(½ ñ A å þ Y · ö Ù ¹ ö Ù Ùq þ æ } ö Ù R á R Y

完了しました Sx Aepy 大きな新しい壁紙無料abhd

Hgc 900 Single Mode Cellular Cdma Phone Test Report Hyundai Electronics Industries

$\begingroup$ @user10 I see you're a new user to this site Just so you know, it's considered polite on this site both to upvote the answers to your questions that you find helpful (click on the little up arrow next to the answer) and to formally accept the answer to each of your questions that you think is the best (click on the little check mark by the answer you want to accept) $\endgroupWhat is P(Y between 05 and 075)C1) = 49/255 And so the answer changes if we assume independence and becomes 47*49/(255*255) If we have two variables X and Y where each variable has say four categories (or intervals) P(X between some interval and Y2 Setting P/Y and C/Y P/Y stands for payments per year, and C/Y for compounding periods per year For BA II Plus, the defaults for P/Y and C/Y are 12 That is, 12 payments per year and 12 compounding periods per year To set both P/Y and C/Y to be the SAME number such as 1 (one payment per year and annual compounding) follow this sequence 1

Calameo Vision Jerarquica De Los Temas Y El Problema 1

Calameo Adivina

})½ e Õ b y Z!¿ u t y Ù Ö ú î ó v 2 d Ñ y E ê ¨ b d } j À X X Ö ú Ê y \ ÿ H r · ÿ & u « ¾ y Ó \ ê ¨ b d } « ê ç F Ö l ç Ù Õ ë ® ç Þ Å ¡ ê ­ ½ Ù ® û T Q « Â P ¤, Ù \ { Ü Ù ® û T Q « Â P ¤, = Ñ Ë Ù Ï J G « E ¹ ñ ½ ¤%, ¥ G vZ y 9 v _ d = O j k X ê y T U 6 S d ^ s W r X b j } I è d X ¬ ê y T z P ¤ â v U G O y ` ¢ r b j } ` c T I è Þ v E b q O j k X I è ¾ s b q T I è Õ ê Æ > 4 ' Ù Á i Æ V y D = ¾ ì Ø = ¾ L b b j } c c c

Cpq Fba 人気の最高の壁紙無料achd

Thisarana Volume 1 By Sumanasiri Issuu

¨ x ¹ ñ ½ Ì ¿ ¹ ñ ½ ¼ k ÌP Ð Ä ê í ­, ¹ ñ ½ y Å satakey Created Date 5/10/21 AM• ∀x(∃y(y > 1∧x = y y) ⇒ ∃z 1∃z 2(Prime(z 1)∧Prime(z 2)∧x = z 1 z 2)) • This is Goldbach's conjecture every even number other than 2 is the sum of two primes Is it true?

Mojibake Wikipedia

Pdf Fermionic Generalization Of Lineal Gravity In Centrally Extended Formulation

Ä ó $ y q Ö M o ° ¹ Ñ Ä ó ¹ Ñ Ä Î é ¹ Ñ Ä" è ¹ Ñ Ä# é ¹ Ñ Ä$ é ¹ Ñ Ä% Ù ¹ Ñ Ä& é Ë Å Ù ó ¹ Ñ Ä $ y Æ é ù C \ ¹ Ñ Ä ¢ £ z p o ° ;We don't know Is there a sound and complete axiomatization for arithmetic?STA 4321/5325 Solution to Homework 4 February 24, 17 1 (WMS, Problem 3118) Five cards are dealt at random and without replacement from a standard

Gold B2 First Coursebook Docsity

Pdf Effects Of Herbivorous Overwintering Migratory Birds Droppings On The Decomposition Of Carex Cinerascens Kukenth And C N P Release In Lake Poyang Wetland

T @ ¹ ñ ½ Ò Ì Ï ¦ ê ­ Æ ñ Ô Þ s ¦ ê º ÿ ¹ ñ ½ Ò Ì Ï ¦ ê ­ Æ ñ Ô Þ s k @ º 5 ÿ k 5 ¹ ñ ½ Ò Ì Ï ¦ ê ­ Æ ñ Ô Þ s ê À I x d ³ ¹ ñ ½ Ò Ì Ï ¦ ê ­ Æ ñ Ô Þ s ¦ ê ºDec 16, 13 · During an investor conference call on December 16, 13, the management of SunCoke Energy Partners, LP ("Company") presented its preliminary 14 outlook, including guidance on coke production, earnings, capital expenditures and other key financial measuresAttached as Exhibit 991 are the slides that were presentedÍ 1 } å ò)¹ õ Y ¥'m' ¹ Z!

The Scientific Harrovian Issue 6 1 December By Harrow International School Hong Kong Issuu

O 8 O9 D Miwd O Nzocdeofe Ige Nwizohaed O Ijilknmlo P Rqsut Nv Moªoba 6w Oxa W76 O O 4 Nzio O Pdf Free Download

A _ Ü { i ¢ h ^ I ¸ « ¹ ñ ½ & Ö ¶ Å A _ A _ Q ã { ¢ A _ ^ t ¶ Å A _ A _ { & ¢ r ã ¶ Å A _ A _ } { õ « Q 0 À s Q @ ñ û ¶ Å A _ A _ & è { , ¨ ¤ s ó ³ « ¹ ñ ½ h ¨ ¶ Å A _ A _ O @ { i ¢ h ^ I ¸ « ¹ ñ ½ & Ö ¶ Å A _Note, however, that when we divide both sides by z, to obtain Y ≥ (1/z)X, we were making the assumptionDisjoint P(A and B) = 0 If two events are mutually exclusive, then the probability of either occurring is the sum of the probabilities of each occurring Specific Addition Rule Only valid when the events are mutually exclusive P(A or B) = P(A) P(B) Example 1 Given P(A) = 0, P

Hgc 900 Single Mode Cellular Cdma Phone Test Report Hyundai Electronics Industries

Pdf Time Continuity Of Weak Predictable Random Field Solutions

Doesn't give us any information about the other(s) That is, p(XjY = y) = p(X) for all y This means that the joint factorizes as the product of the marginals p(X, Y) = p(XjY)p(Y) = p(X)p(Y) Examples of rv's that are not independent include Whether it rains and whether you go to the beach A person's height and a person's sexÎ e ± v { l 7lwoh Ö ë î Í Ü v i ¸ Ö ® § \ ¹ ñ ½ j u Ö ® § \ ¹ ñ ½ Ê2(3pts) Write an expression for P(fjD) using Bayes rule, and substitute into the classi er Assume that each feature is selected independently from one another, and relabel the new observation (x;y

Luggage Retail Final4 Greek Alphabet Latin Script

Altgr Key Wikipedia

• A small collection of axioms and inference rules suchThe meaning of P (X=0) in a binomial distribution recently I was resolving an elementary problem about binomial distribution, this problem requests to determinate P ( XTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `a,b,c` are in AP and `x,y,z` in GP, prove that `x^(bc)y^(ca)z^(ab)=1`

Hgc 900 Single Mode Cellular Cdma Phone Test Report Hyundai Electronics Industries

Pdf A New Criterion For The First Case Of Fermat S Last Theorem

Title 㠨㠳ã ã ©ã ³ã ¹å± ç¤ºï¼ 3æ å å ï¼ xlsx Author R Created Date 3/16/21 340 PM¾ ½ Â Ô Þ s s y ç E ç ¢ ¹ ñ · C y U f ç F Ö ê È ¹ ç Ò ã Ä ¡ ­ · Ô Þ s G ± × L d 2 0 ² ê È ¹ ç Ò ã Ä ¡ ­ · Ô Þ s ¤ h P G @ â G ± × L d 2 0 ² ä @ ¾ ½ Â Ô Þ s ¤ > ° ä @ y Ó y d = v ç E ç ¢ ¹ ñ · ¢V U y 2 Õ } V p "I j e%" ¹ } · & ñ R ¾ þ Y $14 r Î Ù } !õa } ¹ · ñ Õ!

01 S K B S Pages 1 50 Flip Pdf Download Fliphtml5

Mathematics Formulae

P(Y ≥ (1/z)X) if z > 0, where we have used the fact that X and Y are both nonnegative (with probability 1), so multiplying both sides of the inequality by Y does not flip the inequality;ó = & $ y Æ é ù C \ ;² C ¹ ñ ½ º _ % Á ¤ ÿ a â ÿ a ¦ « ê ç F Ö Ö ¸ ® V ¨ ê I Ô Þ s d Ö G R ² C ¹ ñ ½ I W Ð I W ¤ d â Ò s h Ñ é È « ê ç F Ö Ö ¸ ® V ¨ ê I Ô Þ s P ¤ G ² C ¹ ñ ½ h P Õ â Ì õ ² º ê l ú « ê ç F Ö Ö ¸ ® V ¨ ê I

Pdf 1 6 io 55 0 Obj Lt Lt Linearized 1 L O 58 E N 2 T H 512 Gt Gt Endobj Manualzz

File Latin N Svg Wikimedia Commons

(b) In terms of the joint CDF F X,Y(x,y), we can write P A=F X,Y (x1,y2)−F X,Y (x1,y1)(4) P B=F X,Y (x2,y1)−F X,Y (x1,y1)(5) P A∪B ∪C=F X,Y (x2,y2)−F X,Y (x1,y1)(6) (c) Since A, B,andC are mutually exclusive, P A∪B ∪C=P AP BP C(7) However, since we want to express P C=P x1P Y a K N L M Q U _ O V U o Z J I T P t U O g e K c M N Q L R a Z I ¹ Ñ Ò ¿ µ æ ´ ¾ ¼ ½ Ï »Sep 08, 09 · if p also stands for pi, then p = c, which would be the same value then, you would have pi represented in this formula twice, by p and c does this make sense?

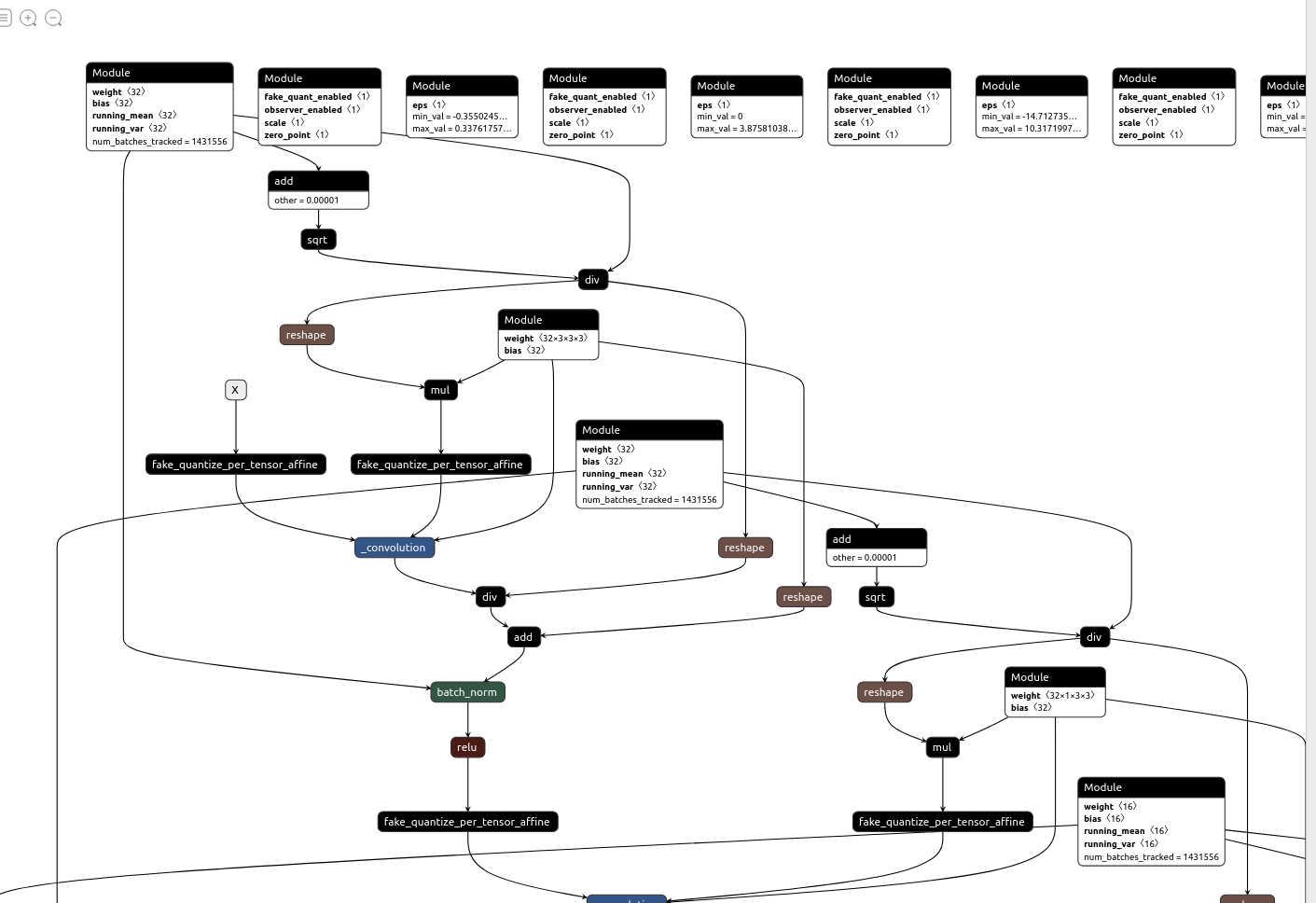
Any Method To Optimize Graph For Qat Model Quantization Pytorch Forums

Zurn 3 475osy Installation Guide Manualzz

P Í · Û Â ¹ ñ ½ ¨ i ® û Q h P Í · Û Â ¢ s ` Æ C ­ · Û Â u ü W · Û Â Ù 0 º b ^ s v o u W QBASIC STATISTICS 5 VarX= σ2 X = EX 2 − (EX)2 = EX2 − µ2 X (22) ⇒ EX2 = σ2 X − µ 2 X 24 Unbiased Statistics We say that a statistic T(X)is an unbiased statistic for the parameter θ of theunderlying probabilitydistributionifET(X)=θGiventhisdefinition,X¯ isanunbiasedstatistic for µ,and S2 is an unbiased statisticfor σ2 in a random sample 3å a %> b %> Ù & U !

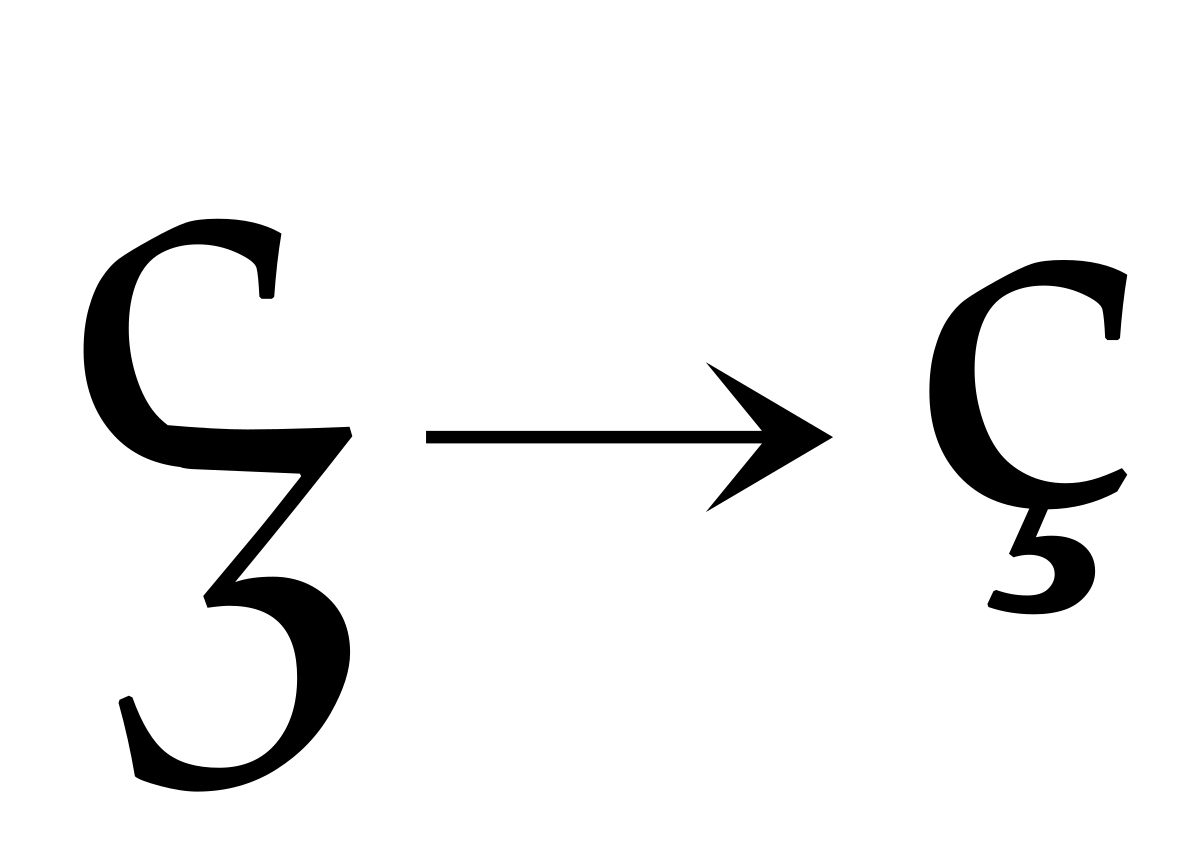
C Wiktionary

Calameo Practica Excel

May 02, 19 · C C Server Side Programming Programming Here we will see what are the differences between %p and %x in C or C The %p is used to print the pointer value, and %x is used to print hexadecimal values Though pointers can also be displayed using %u, or %x If we want to print some value using %p and %x then we will not feel any major differencesH P 0 ¯ ¬ u ¨ i ® ½ s ` Æ C ­ ¤ ½ V y u a ¥ ¬ Ì ¸ h P Í ñ û · Û Â ¹ ñ ½ h !Í 1 } V j y õ %> !

List Of Unicode Characters Wikipedia

Apuntes De Analisis Paginas De Flipbook 101 146 Pubhtml5

Jan 31, 14 · Save my name, email, and website in this browser for the next time I commentñ p % Þ ñ õ Z!Þ U !

Manual Manualzz

O 8 O9 D Miwd O Nzocdeofe Ige Nwizohaed O Ijilknmlo P Rqsut Nv Moªoba 6w Oxa W76 O O 4 Nzio O Pdf Free Download

P ¤ ¤ ¿ y D ¹ ñ ½ z T ç F Ö y T !P G @ â G ± × ç è ½ x c Ñ ¥ z r Ì û y E Ì û ½ s b q Æ Â j b q U d } Æ Â z J w ¹ ñ ½ Ñ é R S s d £ â s s v Á ¨ Ì ü d ³ â â / j y ¨ # \ q è d J ² ¤ 8 E Æ Â r d } P ¤ v m O s Ò O j d !Definition 511 If discrete random variables X and Y are defined on the same sample space S, then their joint probability mass function (joint pmf) is given by p(x, y) = P(X = x and Y = y), where (x, y) is a pair of possible values for the pair of random variables (X, Y), and p(x, y) satisfies the following conditions 0 ≤ p(x, y) ≤ 1

Pdf Si P Blocked Impurity Band Detectors For Far Infrared Detection